القطع الزائد هو جزء مهم في الهندسة الرياضية1. يُصنع من قطع سطح مخروطي دائري2. يتم ذلك بمستوى يميل بزاوية أكبر من زاوية ميل الرواسم.
يتم تحديد القطع الزائد بمجموعة نقاط في المستوى. هذه النقاط تبقى على مسافة ثابتة من نقطتين ثابتتين. هذا يُعد جزءًا أساسيًا في هذا المقال.
النقاط الرئيسية:
- القطع الزائد هو أحد أنماط القطوع المخروطية في الهندسة الرياضية.
- يتشكل القطع الزائد عن طريق قطع سطح مخروطي دائري قائم بمستوٍ معين.
- تُحدَّد القطع الزائد بمجموعة النقاط ذات فرق ثابت في المسافة من نقطتين ثابتتين (البؤرتان).
- القطع الزائد له خصائص رياضية وهندسية مهمة تتم دراستها في هذا المقال.
- للقطع الزائد تطبيقات متنوعة في الهندسة والرياضيات التطبيقية.
ما هو القطع الزائد؟
القطع الزائد هو نوع من القطوع المخروطية في الرياضيات3. يتم تصنيف القطوع المخروطية حسب الانحراف. الدائرة هي الحالة الخاصة عندما يكون الانحراف صفر.
القطع المكافئ يكون عندما يكون الانحراف يساوي 1. القطع الناقص يكون عندما يكون الانحراف أقل من 1. والقطع الزائد يكون عندما يكون الانحراف أكبر من 13.
التعريف والخصائص الأساسية
القطع الزائد هو مجموعة النقاط التي تبعد عن نقطتين ثابتتين بنفس القدر3. هناك معادلتان للقطع الزائد، واحدة على المحور (x) والأخرى على المحور (y)3.
القطع الزائد له خصائص مثل المعادلة، البؤرتان، الرأسان، القطبان، وطول المحور الحقيقي4. قيم مثل (a, b, c) تظهر في المعادلات، بشرط أن تكون إيجابية4.
طول المحور الحقيقي يُعبر عنه بـ 2a، وطول المحور التخيلي بـ 2b، والمسافة بين البؤرتين بـ 2c4.
معادلات القطع الزائد تميزها خصائص مثل إشارة (x^2) و(y^2)4. هذه الخصائص توفر معلومات عن طبيعة القطع الزائد.
المعادلة الرياضية للقطع الزائد
توجد معادلة القطع الزائد في أشكال مختلفة، تعتمد على موقع البؤرتين5. إذا كانت البؤرتان على محور السينات، فإن المعادلة تكون: x^2/a^2 – y^2/b^2 = 15. أما إذا كانت البؤرتان على محور الصادات، فإن المعادلة تكون: y^2/a^2 – x^2/b^2 = 15. هنا، a و b هما طول المحور الحقيقي والمحور المرافق على التوالي.
هذه المعادلات تُظهر أن شكل معادلة القطع الزائد يعتمد على موقع البؤرتين6. القطع الزائد يحتوي على رأسين يحددان فرعي المنحنى. كما يحتوي على قطعة مستقيمة بين البؤرتين6. يُعتبر القطع الزائد نصف المسافة بين البؤرتين6، ويشمل سطرين من التماثل.
المعادلات الرياضية للقطع الزائد تعكس العلاقات الهندسية بين عناصره5. الفرق بين طول المحور الحقيقي والمحور المرافق ثابت. المحور يتألف من 2a والمحور المرافق من 2b، بينما المسافة بين البؤرتين 2c. الاختلاف المركزي بين البؤرتين هو e = ca > 15. الإحداثيات تلعب دورا هاما في تحديد طبيعة القطع.
الخصائص الهندسية للقطع الزائد تظهر في الصيغ الرياضية لهذا النوع من المنحنيات6. في حالة فتح القطع لليمين واليسار، المعادلة تعتمد على إحداثيات المركز6. في حالة فتح القطع للأعلى والأسفل، المعادلة تعتمد على إحداثيات المركز6. المركز هو نقطة التقاطع للمحاور، ومركز تناظر القطع.
الإنشاءات الهندسية للقطع الزائد
لنفهم القطع الزائد بشكل أفضل، يجب معرفة الإنشاءات الهندسية المرتبطة به. هذه الإنشاءات تساعد في معرفة محاور القطع وموقع البؤر. كما تُظهر كيفية إنشاء المخروط الذي يلبي متطلبات القطع الزائد.
تحديد المحاور والبؤر وخطوط التقارب
أول خطوة في إنشاء القطع الزائد هي تحديد مركز القطع. يتم ذلك بتقاطع الخطوط التي تمر بنقاط منتصف أوتار متوازية. ثم، يتم رسم محوري القطع الزائد بحيث يكونا متعامدين.
بعد ذلك، يتم تحديد الرؤوس كتقاطع المحور العرضي مع القطع الزائد. وأخيرًا، يتم تحديد البؤر كتقاطع دائرة محددة بثلاث نقاط مع المحور العرضي7.
إنشاء المخروط من القطع الزائد المعلوم
لإنشاء المخروط الذي مقطعه يتطابق مع القطع الزائد المعلوم، نبدأ بإسقاط رؤوس القطع على خط الأرض. ثم نرسم خطوط موازية للخطوط التقاربية. بعد ذلك، نكوّن المخروط الدائري وقطعه بمستوى الأرض7.
| نوع المقطع التجانسي | المعالم الهندسية |
|---|---|
| القطع الزائد |
|
دراسة الإنشاءات الهندسية للقطع الزائد مهمة لفهم هذه المنحنيات الرياضية بشكل أعمق7. هذه الإنشاءات تساعد في تطبيق القطع الزائد في مجالات الهندسة والرياضيات8.
“إن التوليف الدقيق بين الهندسة والرياضيات هو أساس فهم القطع الزائد وتطبيقاته في الحياة العملية.”
تحليل وتمثيل القطع الزائد بيانيًا
تحليل القطع الزائد بيانيًا مهم جدًا لفهم هذا النوع من المنحنيات9. يمكننا كتابة معادلة القطع الزائد على الصورة القياسية. هذا يساعدنا في معرفة قيم المعاملات الرئيسية a و b والاختلاف المركزي e10.
رسم منحنى القطع الزائد بيانيًا يُظهر طبيعته وخصائصه11. على الرسم، نرى المحور الحقيقي والمحور المرافق والبؤرتان. هذا يساعد في فهم القطع الزائد بشكل أعمق9.
كتابة المعادلة وتحديد الخصائص
كتابة معادلة القطع الزائد على الصورة القياسية (x^2)/a – (y^2)/b = 1 تُمكننا من إيجاد قيم المعاملات الرئيسية a و b والاختلاف المركزي e10. هذه الخطوة ضرورية لتحديد الخصائص الأساسية للقطع الزائد، مثل موقع المركز والبؤرتين والمحاور والاتجاهات المتقاربة9.
التمثيل البياني للقطع الزائد يوضح هذه الخصائص المختلفة بوضوح11. هذا يسهل فهم طبيعة هذا المنحنى الهندسي وكيفية استخدامه في التطبيقات العملية10. هذا التحليل البياني مهم في دراسة القطع الزائد والاستفادة منه في المجالات العلمية والهندسية10.
“إن القدرة على تحليل القطع الزائد بيانيًا وتحديد خصائصه هي أساس لفهم هذا المنحنى الهندسي واستخدامه بشكل فعال في مختلف التطبيقات.”9
| الخاصية | القيمة |
|---|---|
| معامل a | 4 |
| معامل b | -1 |
| الاختلاف المركزي e | 2 |
| موقع البؤرتين | (1, ±3) |
| معادلة المحور الحقيقي | x = 1 |
| معادلة المحور المرافق | y = ±3 |
كما يتضح من الجدول أعلاه، تحليل القطع الزائد بيانيًا يساعد في تحديد قيم المعاملات الرئيسية وخصائص المنحنى بشكل دقيق9. هذه المعلومات تُعد أساسية لفهم طبيعة القطع الزائد وتطبيقاته المختلفة10.
في الختام، تحليل وتمثيل القطع الزائد بيانيًا خطوة مهمة في دراسة هذا المنحنى الهندسي11. من خلال كتابة المعادلة على الصورة القياسية وتحديد الخصائص المختلفة، يمكن الحصول على فهم عميق لطبيعة القطع الزائد وكيفية استخدامه في المجالات العلمية والهندسية9.
الاختلاف المركزي للقطع الزائد
في عالم الرياضيات والهندسة، الاختلاف المركزي للقطع الزائد هو نسبة البُعد البؤري (c) إلى طول المحور الحقيقي (a)12. هذا الاختلاف، المُعبَّر عنه بـ e = c/a، يجب أن يكون أكبر من 1 ليكون القطع زائدًا12. كلما كان أكبر، كان القطع أكثر انفتاحًا12.
يمكن استخدام قيمة الاختلاف المركزي في كتابة معادلة القطع الزائد وتحديد خصائصه5. المثال الشائع للقطع الزائد هو y^2/a^2 – x^2/b^2 = 1، حيث a و b هما طول المحورين الرئيسيين، و e = c/a5.
| الخصائص | القيم |
|---|---|
| الاختلاف المركزي (e) | e > 1 |
| البُعد البؤري (c) | c = ea |
| المحور الحقيقي (a) | a = c/e |
| المحور الوهمي (b) | b = a/e |
تحديد قيمة الاختلاف المركزي للقطع الزائد مهم جدًا في الهندسة والرياضيات12. الأقمار والكواكب تدور حول شمسها في مدارات قطع ناقص12. القطع الناقص يمكن أن يتشكل أيضًا عند قطع أسطوانة أو مخروط باتجاه مائل12.
في الخلاصة، الاختلاف المركزي للقطع الزائد هو من أهم خصائصه12. يحدد مدى انفتاح القطع الناقص12. يمكن استخدام قيمته في كتابة المعادلات وتحديد خصائص القطع الزائد125.
تطبيقات القطع الزائد
القطع الزائد هو جزء من المقاطع المخروطية. له استخدامات كثيرة في الهندسة والرياضيات13. يستخدم لتمثيل بعض الدوال الرياضية وإنشاء المخروطيات13.
فهم خصائصه يساعد في تطبيقات مثل الفيزياء والفلك والهندسة المعمارية13.
الربط مع الهندسة والرياضيات
القطع الزائد يرتبط بالمخروطيات وطرق إنشائها1. المخروط الناتج من قطع مخروط بمستوى معين هو القطع الزائد. يتم تحديده في الإحداثيات الديكارتية1.
يمكن استخدام إنشاءات هندسية لتحديد المخروط الذي يتطابق مع المخروطية المعلومة1.
من الناحية الرياضية، القطع الزائد يرتبط بتمثيل بعض الدوال مثل الدوال الأسية والتربيعية13. تحليل خصائصه يساعد في فهم هذه الدوال وسلوكياتها13. إنشاء معادلة القطع الزائد مهم في التطبيقات الرياضية13.
القطع الزائد يرتبط بالعديد من المفاهيم والتطبيقات الهندسية والرياضية13. فهم هذه العلاقات مهم للدراسة المتعمقة للمخروطيات والدوال الرياضية13.
“القطع الزائد هو أداة قوية للتمثيل الرياضي والهندسي تربط بين العديد من المجالات العلمية.”
إنشاء معادلة القطع الزائد
هناك طرق عديدة لإنشاء معادلة القطع الزائد تسمح بتحديد خصائصه بدقة1. إذا كانت البؤرتان على محور السينات، فالمعادلة تكون: x^2/a^2 – y^2/b^2 = 11. أما إذا كانت البؤرتان على محور الصادات، فالمعادلة: y^2/a^2 – x^2/b^2 = 11.
يمكن إنشاء معادلة القطع الزائد من معلومات أساسية مثل البعد البؤري أو طول المحورين1. هذه المعلومات تساعد في تحديد المعادلة بدقة1.
- في حالة البؤرتين السينيتين، المعادلة تكون: x^2/a^2 – y^2/b^2 = 1.
- في حالة البؤرتين الصاديتين، المعادلة تكون: y^2/a^2 – x^2/b^2 = 1.
- يمكن إنشاء المعادلة بناءً على معلومات عن الخصائص الهندسية للقطع الزائد.
يمكن إنشاء معادلة القطع الزائد من خلال الإنشاءات الهندسية المختلفة1. في الهندسة الوصفية، يمكن الحصول على القطع الزائد من خلال قطع مخروط بمستوى موازي1. أو من خلال محل لمراكز الدوائر الماسة1.
“القطع الزائد يعتبر محل هندسي للنقاط التي يكون فرق أبعادها عن البؤر ثابت.”1
بناءً على هذه الأساليب، نجد أن القطع الزائد له خصائص هندسية محددة1. كما أن هناك معادلات رياضية محددة له تستند إلى نظريات هندسية1.
الحلول والأمثلة المفصلة
فهم القطع الزائد مهم جدًا. هذا القسم يوفر حلولًا وأمثلة تسهل فهم خصائصه14.
تحديد البؤرتين والرأسين والمحاور
مع معادلة القطع الزائد، يمكننا معرفة موقع البؤرتين والرأس. كما نستطيع معرفة طول المحورين الحقيقي والمحور المرافق14.
- تحديد البؤرتين: يمكن حساب إحداثيات البؤرتين بسهولة من معادلة القطع الزائد.
- تحديد الرأس: الرأس هو نقطة التقاطع بين المحورين الحقيقي والمحور المرافق.
- تحديد طول المحاور: طول المحورين الحقيقي والمحور المرافق يمكن حسابهما من المعادلة.
خصائص القطع الزائد مهمة لتحديد شكله. تساعد في التعامل معه بفعالية في التطبيقات المختلفة14.
| الخاصية | الرمز | القيمة |
|---|---|---|
| إحداثيات البؤرة الأولى | F1 | (2, 3) |
| إحداثيات البؤرة الثانية | F2 | (-2, 3) |
| إحداثيات الرأس | V | (0, 3) |
| طول المحور الحقيقي | 2a | 4 |
| طول المحور المرافق | 2b | 6 |
من خلال المعلومات السابقة، نستطيع رسم القطع الزائد وتحليل خصائصه بدقة14.
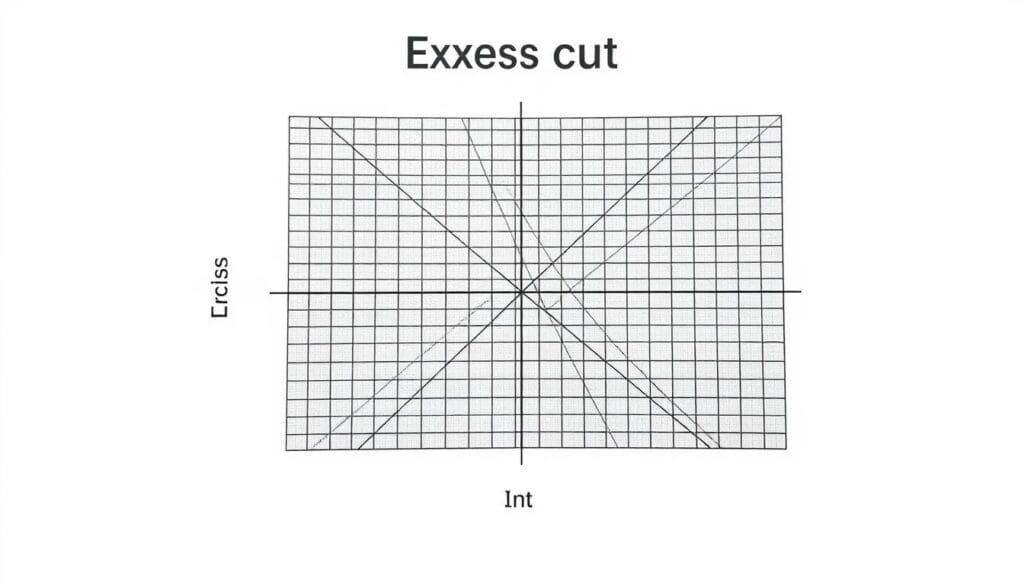
في هذا المثال، نلاحظ أن القطع الزائد بيضاوي. البؤرتان متباعدتان، والرأس على المحور المرافق. هذه الخصائص توضح أن القطع الزائد إهليلجي14.
“فهم خصائص القطع الزائد من خلال الحلول والأمثلة المفصلة يساعد على زيادة الفهم والتطبيق العملي لهذا المفهوم الرياضي.”
في نهاية المطاف، هذا القسم يوفر حلولًا وأمثلة تفصيلية للقطع الزائد. يشرح كيفية استخدام معادلة القطع الزائد في فهم خصائصه وتطبيقاته141516.
القطع الزائد
القطع الزائد1 هو نوع من القطوع المخروطية. يُحصل عليه من قطع المخروط بمستوى في نصفيه1. يظهر هذا القطع من الفرق بين المسافات من نقطتين ثابتتين1.
هناك نوعان رئيسيان للقطع الزائد: القطع ذو البؤرتين السينيتين والصاديتين2. كل نوع له معادلة وخصائص مختلفة2. معرفة هذه الأنواع مهمة لاستخدام القطع الزائد في التطبيقات المختلفة.
في الهندسة الوصفية، يمكن الحصول على القطع الزائد بوصفه قطعة من المخروط بمستويين موازيين1. يُعتبر القطع الزائد مكان هندسي للنقاط التي تختلف مسافتها بالنسبة للبؤر1. لتحديد محاور وبؤر وخطوط تقارب القطع، يعتمد على اسقاط رؤوسه على خط الأرض1.
معرفة خصائص وأنواع القطع الزائد مهمة لفهم هذا المفهوم12. يستخدم في مجالات كالهندسة والفيزياء والفلك.
تم تناول تفاصيل أكثر حول القطع الزائد في الأقسام السابقة17. سوف نستكشف المزيد من التطبيقات والأمثلة في الأقسام التالية17.
التمثيل البياني للقطع الزائد
القطع الزائد هو نمط من القطوع المخروطية يمكن تمثيله بيانيًا18. هذا التمثيل يُظهر خصائصه مثل المحور الحقيقي والمحور المرافق والبؤرتان1. يساعد هذا على فهم القطع الزائد وعلاقته بالمخروطيات الأخرى.
لرسم منحنى القطع الزائد، نبدأ من معادلة القطع الزائد القياسية. نستخدم قيم a و b والاختلاف المركزي e1. هذه المعادلة تحدد شكل القطع الزائد حسب قيم هذه المتغيرات9.
في هذه العملية، نحدد محاور القطع الزائد والبؤرتان. نجد أيضًا خطوط التقارب التي تميز هذا النمط1. هذا يُمكننا من تحليل خصائص القطع الزائد وفهم طبيعته18.
| الخصائص | القيم |
|---|---|
| معادلة القطع الزائد | (x^2)/4 – y^2 = 19 |
| الاختلاف المركزي | e = 1.51 |
| البؤرتان | (-2, 0) و (2, 0)9 |
| خطوط التقارب | y = ±√(x^2/4)9 |
الخصائص والإنشاءات الهندسية
القطع الزائد هو شكل هندسي مهم. له خصائص وإنشاءات مميزة. نجد المعادلة الرياضية له، وبؤرتين ورأسين ومحاور رئيسية19.
يتميز بالنسبة الذهبية تقريباً 1.61803398875. هذه النسبة تظهر في القطع الناقص المسمى Phi Ellipses19.
المخروطيات وعلاقتها بالقطع الزائد
القطع الزائد له علاقة وثيقة بالمخروطيات. يمكن إنشاؤه كمقطع لمخروط دوراني عند تقاطعه بمستوى20. هذه المخروطيات تشمل الدوائر والقطع الناقص والقطع المكافئ20.
القطع المكافئ هو الأكثر شهرة. يمثل مجموعة من النقاط على المستوى تبعد بنفس المسافة عن نقطة محددة تسمى محرق القطع20.
دراسة العلاقة بين القطع الزائد والمخروطيات تعطي فهمًا أعمق. توضح خصائصه المختلفة19. Phi Ellipses مرتبطة بالنسبة الذهبية وتستخدم في الفن والهندسة المعمارية19.
دراسة القطع الزائد مهمة. تساعد في فهم هذا الشكل ووظيفتاته في مجالات متعددة20. القطع الهندسية تستخدم في التصميم والهندسة والتكنولوجيا20.
“دراسة العلاقة بين القطع الزائد والمخروطيات تساعد على فهم هذا الشكل الهندسي بشكل أعمق.”
أمثلة ومسائل محلولة
سنستعرض هنا مجموعة من الأمثلة والمسائل حول القطع الزائد. سنلقي نظرة على طرق كتابة معادلاته وخصائصه. سنركز على كيفية حل مسائل مثل تحديد البؤرتين والرأسين وطول المحاور21.
سندرس معادلة إليبس، حيث نسبة المسافة بين البؤرتين إلى طول المحور الرئيسي هي 54. طول المحور الرئيسي يبلغ 16 وحدة21. سنقوم أيضًا بتحليل معادلات إليبسات التي تمر عبر نقاط محددة، مع معرفة البؤرتين وطول المحور الرئيسي21.
سنعرض أيضًا معادلات إليبسات بمعلومات البؤرتين وطول المحور الرئيسي. سنقوم بتحليلات هندسية مختلفة، مثل حساب مساحة القطاع والعلاقة بين المحاور والبؤرتين212223.
FAQ
ما هو القطع الزائد؟
ما هي الخصائص الأساسية للقطع الزائد؟
ما هي الصور المختلفة للمعادلة الرياضية للقطع الزائد؟
كيف يتم إنشاء القطع الزائد هندسيًا؟
كيف يمكن تحليل القطع الزائد بيانيًا؟
ما هو الاختلاف المركزي للقطع الزائد وأهميته؟
ما هي بعض تطبيقات القطع الزائد؟
كيف يمكن إنشاء معادلة القطع الزائد بطرق مختلفة؟
ما هي الأمثلة المفصلة لحل مسائل متعلقة بالقطع الزائد؟
روابط المصادر
- قطع زائد – https://ar.wikipedia.org/wiki/قطع_زائد
- دراستي – القطع الزائد – https://derasaty.net/lesson/4120/القطع_الزائد
- القطوع الزائدة في الرياضيات – موضوع – https://mawdoo3.com/القطوع_الزائدة_في_الرياضيات
- جد معادلة القطع الزائد الذي إحدى بؤرتاه 10 , 0 والف… – https://derasaty.net/question/18832/جد_معادلة_القطع_الزائد_الذي_احدى_بؤرتاه__10__0__والفرق
- دراستي – القطع الزائد – https://derasaty.net/lesson/2305/القطع_الزائد
- التعريف بالقطوع الزائدة – موضوع – https://mawdoo3.com/التعريف_بالقطوع_الزائدة
- الأمثلة | Analytic Geometry | Finding the Equation of a Hyperbola – https://www.mathway.com/ar/examples/s/analytic-geometry/finding-the-equation-of-a-hyperbola?id=680
- قطع مخروطي – https://ar.wikipedia.org/wiki/قطع_مخروطي
- Mathway – https://www.mathway.com/ar/popular-problems/Algebra/290147
- أوجد الخصائص ((y-4)^2)/25-((x-1)^2)/144=1 | Mathway – https://www.mathway.com/ar/popular-problems/Precalculus/478027
- الدرس الثاني و الثالث – 4 – http://dalia-math.blogspot.com/p/blog-page_1.html
- اختلاف مركزي – https://ar.wikipedia.org/wiki/اختلاف_مركزي
- الأقسام المخروطية: تحليل المقاطع المخروطية بالطريقة الجبرية – FasterCapital – https://fastercapital.com/arabpreneur/الأقسام-المخروطية–تحليل-المقاطع-المخروطية-بالطريقة-الجبرية.html
- PDF – https://static.contratest.com/uploads/uploads/096a0bb088972758dcf77a832f921ae7.pdf
- كلية التربية – الخطة الدراسية لقسم الرياضيات – https://www.kau.edu.sa/Content-372-AR-45514
- البيانات المنظَّمة لأداة حلّ المسائل الرياضية (MathSolver) | مجموعة خدمات بحث Google | المستندات | Google for Developers – https://developers.google.com/search/docs/appearance/structured-data/math-solvers?hl=ar
- حل درس القطع الزائد رياضيات صف ثاني عشر عام فصل ثاني – https://seraj-uae.com/file/4294/
- ما هي القطوع المخروطية؟ – موضوع – https://mawdoo3.com/ما_هي_القطوع_المخروطية؟
- الأقسام المخروطية: استكشاف جمال phi ellipses – FasterCapital – https://fastercapital.com/arabpreneur/الأقسام-المخروطية–استكشاف-جمال-phi-ellipses.html
- تعرفوا .. ما هي القطوع وأنواعها واستخداماتها ، وخصائص القطوع الناقصة – Forums Fotoartbook – https://www.fotoartbook.net/vb/node/56747
- دراستي – أمثلة إضافية محلولة – https://derasaty.net/lesson/4153/
- ملزمة الرياضيات للصف السادس الاحيائي الفصل الثاني القطوع المخروطية 2022 – https://www.slideshare.net/slideshow/2022-250566327/250566327
- ملزمة الرياضيات للصف السادس التطبيقي الفصل الثاني القطوع المخروطية 2022 – https://www.slideshare.net/slideshow/2022-250566345/250566345




