مقاييس النزعة المركزية: التعريف والأنواع والاستخدامات والأهمية
نبذة مختصرة عن مقاييس النزعة المركزية
تُستخدم مقاييس النزعة المركزية في الإحصاءات وعلوم البيانات لوصف توزيع البيانات، وهي تُعد من الأدوات الأساسية في تحليل البيانات. تُعرف مقاييس النزعة المركزية بأنها معاملات تحدد موضع القيمة المركزية لمجموعة من البيانات.
وتستخدم هذه المقاييس للحصول على فكرة عامة عن توزيع البيانات، حيث تُساعد في حساب القيم المركزية المختلفة، مثل الوسط الحسابي والمتوسط الحسابي والمنتصف والوسيط والأوتار الرباعية.
يتيح استخدام هذه المقاييس تحليل البيانات بطريقة فعالة ودقيقة، مما يجعلها من أهم الأدوات التحليلية في علم الإحصاء والبحوث الاجتماعية والطبية والاقتصادية وغيرها.
في هذا المقال، سنتعرف على المقاييس المختلفة للنزعة المركزية وسنوضح كيفية استخدامها لتحليل البيانات بطريقة فعالة.

ما هي مقاييس النزعة المركزية – Measures of Central Tendency؟
تشير مقاييس النزعة المركزية إلى القيمة الممثلة لمجموعة من البيانات. تستخدم هذه المقاييس لتلخيص البيانات بشكل مفيد وتقديم فكرة عامة عن المجموعة. وهناك ثلاثة مقاييس رئيسية للنزعة المركزية هي:
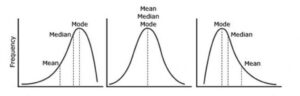
- المتوسط الحسابي (Mean): وهو مجموع القيم في مجموعة البيانات مقسومًا على عددها. يعد المتوسط الحسابي مقياسًا قياسيًا للنزعة المركزية، حيث يعكس القيمة المتوسطة للمجموعة.
- الوسيط (Median): وهو القيمة الوسطية للمجموعة، أي القيمة التي تقع في منتصف البيانات عند ترتيبها من الأصغر إلى الأكبر. يستخدم الوسيط كمقياس للنزعة المركزية عندما يكون هناك تباين كبير في البيانات.
- الوضع (Mode): وهو القيمة الأكثر تكرارًا في المجموعة. يستخدم الوضع كمقياس للنزعة المركزية عندما تكون البيانات متقاربة بشكل كبير، حيث يمثل القيمة الأكثر شيوعًا.
يتم استخدام مقاييس النزعة المركزية بشكل واسع في تحليل البيانات والإحصاءات، ويتم اختيار المقياس الأنسب حسب طبيعة المجموعة المدروسة والهدف من التحليل.

لماذا تُستخدم مقاييس النزعة المركزية؟
تُستخدم مقاييس النزعة المركزية في التحليل الإحصائي للبيانات لتوضيح القيمة الممثلة لمجموعة البيانات. تساعد هذه المقاييس على تحديد وصف الوضع العام للبيانات وفهمها بشكل أفضل. وتتميز المقاييس المركزية بأنها تقدم معلومات عن القيمة المتوسطة للبيانات، مما يساعد في تحديد القيمة التي تمثل الوسط الأكثر تكرارًا أو القيمة المركزية للبيانات.
من بين المقاييس المركزية الشائعة التي تستخدم في التحليل الإحصائي: المتوسط الحسابي، والمتوسط المربعي، والوسيط، والمنتصف، والمود.
تستخدم هذه المقاييس في العديد من المجالات، مثل العلوم الاجتماعية والطبية والهندسية والاقتصادية، ويساعد استخدامها على تحليل البيانات بشكل أكثر فاعلية وفهمها بشكل أفضل. وبالتالي، تلعب المقاييس المركزية دورًا هامًا في البحوث والتحليلات الإحصائية المختلفة.

أهمية مقاييس النزعة المركزية
تعتبر مقاييس النزعة المركزية من أهم المفاهيم الإحصائية المستخدمة في تحليل البيانات، حيث تساعد في فهم وتفسير توزيع البيانات وتحديد مدى تجانسها أو تشتتها. وتشمل مقاييس النزعة المركزية الوسط الحسابي والوسط الهندسي والوسط الهندسي الهندسي والوسط الكمي والوسط المنحني.
تستخدم مقاييس النزعة المركزية بشكل شائع في الإحصاء والتحليل الإحصائي لأنها تمثل قيمة مركزية توضح الموضع النموذجي للمجموعة من البيانات. وتساعد في تحليل البيانات واستخراج المعلومات الهامة منها ومقارنة البيانات ببعضها البعض.
بالإضافة إلى ذلك، تساعد مقاييس النزعة المركزية في تحديد قيمة الانحراف والتشتت في البيانات، حيث يمكن استخدامها لحساب معاملات الانحراف المطلق والانحراف المعياري وتحديد توزيع البيانات بشكل أكبر.
وبشكل عام، فإن فهم مقاييس النزعة المركزية يساعد في فهم توزيع البيانات وتحليلها بطريقة فعالة ودقيقة، مما يجعلها أداة مهمة في العديد من المجالات مثل الأعمال والتجارة والطب والعلوم الاجتماعية والإحصائية.
طالع: أنواع الاحصاء في الرياضيات:التعريف والأنواع والأهمية

اهداف مقاييس النزعة المركزية
تهدف مقاييس النزعة المركزية إلى توفير معلومات حول موقع وتوزيع البيانات في مجموعة من القيم. وتساعد هذه المقاييس في فهم النمط العام للبيانات وتحليلها وتفسيرها.
تحديداً، فإن أهداف مقاييس النزعة المركزية هي:
- تحديد الموضع النموذجي لمجموعة البيانات: وهو القيمة التي تمثل موقع البيانات بشكل عام، مثل الوسط الحسابي أو الوسيط أو الأوّل والثالث الربع.
- تحديد مدى توزيع البيانات حول الموضع النموذجي: وهو يساعد على فهم الانحرافات الكبيرة أو الصغيرة في المجموعة، وذلك من خلال مقاييس مثل الانحراف المعياري أو النطاق.
- تحديد القيم الطبيعية لمجموعة البيانات: وتعني القيم التي يتوقع الحصول عليها في غالبية الأحيان في المجموعة، وذلك من خلال مقاييس مثل الانحراف المعياري.
وبشكل عام، تهدف مقاييس النزعة المركزية إلى توفير معلومات هامة حول توزيع البيانات وتحليلها، مما يمكن أن يفيد في العديد من المجالات مثل الإحصاء والأبحاث الاجتماعية والاقتصادية والطبية وغيرها.
ما هي أنواع مقاييس النزعة المركزية؟
تُستخدم مقاييس النزعة المركزية في الإحصاء لوصف توزيع البيانات ومعرفة المركز الذي يقع حوله البيانات. وتتوفر عدة مقاييس للنزعة المركزية، وأبرز هذه المقاييس هي:
- المتوسط الحسابي (Mean): وهو المجموع الكلي للقيم مقسومًا على عددها، وهو أكثر المقاييس استخدامًا.
- الوسط الحسابي (Median): وهو القيمة التي تقع في منتصف البيانات المرتبة من الأصغر إلى الأكبر.
- الوسيط (Mode): وهو القيمة التي تتكرر أكثر من غيرها في البيانات.
- النسبة المئوية الثانية (Percentile): وهي القيمة التي تقسم البيانات إلى نسبة مئوية محددة، مثل النسبة المئوية الخمسونية التي تقسم البيانات إلى نصفين متساويين.
- الوسط الهندسي (Geometric mean): وهو المتوسط الحسابي للقيم بعد أن يتم ضربها جميعًا ثم جذرها.
- الوسط الهندسي الهندسي (Harmonic mean): وهو المتوسط الحسابي للقيم بعد أن يتم قسمها جميعًا على مقابلاتها العكسية ثم حساب المتوسط الحسابي للنتائج.
يمكن استخدام هذه المقاييس بشكل متباين حسب الغرض من التحليل وخصائص البيانات المُستخدمة، وفي الكثير من الحالات يتم استخدام أكثر من مقياس في الوقت نفسه للحصول على صورة شاملة للبيانات.
انظر: تحليل التباين ANOVA
ما هي أنواع مقاييس التشتت في البحث العلمي؟
هناك عدة أنواع من مقاييس التشتت المستخدمة في البحث العلمي، ومن بين هذه المقاييس:
- الانحراف المعياري (Standard Deviation): وهي قياس لقوة تباين البيانات حول المتوسط الحسابي للعينة، حيث يتم حساب قيمة الانحراف المعياري بالطريقة التالية:
– يتم حساب متوسط العينة.
– يتم حساب الفرق بين قيمة كل عنصر في العينة والمتوسط.
– يتم رفع هذه الفروق إلى الأس الثاني وحساب المتوسط الحسابي لها.
– يتم حساب الجذر التربيعي للقيمة المستخرجة من الخطوة السابقة، وهي الانحراف المعياري.
- المدى (Range): وهو قياس يوضح فرق أكبر قيمة وأصغر قيمة في العينة.
- الانحراف المتوسط المطلق (Mean Absolute Deviation): وهو قياس يعطي فكرة عن مقدار التباين في العينة، ويتم حسابه عن طريق حساب المتوسط الحسابي للفروق المطلقة بين كل قيمة في العينة والمتوسط الحسابي للعينة.
- متوسط الانحراف المربعي (Mean Squared Deviation): وهو قياس يحسب مقدار التباين في العينة بطريقة مشابهة للانحراف المعياري، ولكن يتم رفع الفروق إلى الأس الثاني وحساب المتوسط الحسابي لها.
يمكن استخدام هذه المقاييس لتقييم التشتت في البيانات، ويتم استخدامها في مجالات مختلفة مثل الإحصاء والأبحاث العلمية والعلوم الاجتماعية والتحليل الاقتصادي.
مثال على حساب مقاييس النزعة المركزية
يستخدم حساب مقاييس النزعة المركزية لتحديد القيمة المركزية لمجموعة من البيانات. وهناك ثلاثة مقاييس مختلفة للنزعة المركزية: الوسط الحسابي (المتوسط)، الوسط المتحرك، والوسط الهندسي.
وإليك مثالًا على حساب كل مقياس في مجموعة الأرقام التالية: 2، 4، 6، 8، 10.
– الوسط الحسابي: يتم حسابه بجمع جميع الأرقام ومن ثم قسمتها على عددها الكلي. في هذه المجموعة، الوسط الحسابي يساوي: (2 + 4 + 6 + 8 + 10) ÷ 5 = 6.
– الوسط المتحرك: يتم حسابه بجمع الأرقام في الفترة المحددة ومن ثم قسمها على عدد الفترات. يمكن أن تكون الفترة هي أي عدد من الأرقام. لهذه المجموعة، سنستخدم فترة 3. الوسط المتحرك الأول هو (2 + 4 + 6) ÷ 3 = 4، الوسط المتحرك الثاني هو (4 + 6 + 8) ÷ 3 = 6، والوسط المتحرك الثالث هو (6 + 8 + 10) ÷ 3 = 8.
بالتالي، الوسط المتحرك يساوي: (4 + 6 + 8) ÷ 3 = 6.
– الوسط الهندسي: يتم حسابه بأخذ جذر عدد الأرقام في المجموعة، ثم ضرب الأرقام معًا ومن ثم رفعها إلى قوة واحدة على عدد الأرقام. لهذه المجموعة، الوسط الهندسي يساوي: √(2 × 4 × 6 × 8 × 10) = 4.38.
مزايا وعيوب مقاييس النزعة المركزية
تستخدم مقاييس النزعة المركزية لتوضيح موقع المتوسط في مجموعة من البيانات. وتعرف بأنها القيمة الأكثر شيوعًا في البيانات، وتشير إلى المركز الذي يوجد به مجموع البيانات. وفيما يلي بعض المزايا والعيوب المتعلقة بمقاييس النزعة المركزية:
مزايا
– تمثل مقاييس النزعة المركزية قيمة مرجعية مفيدة للمقارنة بين مجموعات مختلفة من البيانات.
– تعد الوسيط أو الوسط الحسابي أو الوسط الهندسي أو الوسط الهندسي الهندسي مقاييس مقبولة من قبل العديد من المجتمعات العلمية والتجارية والصناعية.
– يمكن استخدام مقاييس النزعة المركزية لتخطيط البيانات وتحليلها بطريقة سهلة وبسيطة.
عيوب
– قد تكون مقاييس النزعة المركزية حساسة للقيم الشاذة أو القيم المتطرفة، حيث تكون هذه القيم قادرة على تشويه القيم المحسوبة.
– لا يتم توزيع القيم بشكل متساوٍ على الجانبين من المتوسط الحسابي. وقد يكون هذا التحدي أكثر وضوحًا في البيانات ذات الانحراف المعياري الكبير.
– لا يمكن استخدام مقاييس النزعة في التعامل مع المتغيرات الكبيرة أو المجموعات ذات القيم المتعددة والمتغيرة.
بشكل عام، يجب أن يتم استخدام مقاييس النزعة المركزية بحذر وفي سياق التحليل الإحصائي الذي يتم تنفيذه، ويجب عدم الاعتماد على مقياس واحد فقط لتحديد موقع المتوسط في المجموعة.
استخدامات مقاييس النزعة المركزية في حياتنا اليومية
تستخدم مقاييس النزعة بشكل واسع في الحياة اليومية لتلخيص وتحليل البيانات الكمية في مجالات مختلفة. إليك بعض الأمثلة:
1- في المالية: يتم استخدام مقياس الوسط الحسابي لتحليل البيانات المالية مثل الإيرادات والأرباح والخسائر.
2- في الإحصاء: يتم استخدام مقياس الوسط الحسابي والميدان لتلخيص وتحليل البيانات الإحصائية مثل العمر والدخل والوزن.
3- في التعليم: يتم استخدام مقياس الوسط الحسابي لتحليل نتائج الاختبارات والتقييمات الأكاديمية.
4- في الطب: يتم استخدام مقياس الوسط الحسابي والميدان لتحليل البيانات الصحية مثل ضغط الدم ومعدل نبضات القلب والوزن.
5- في الرياضيات: يتم استخدام مقياس الوسط الحسابي والميدان في حساب المتغيرات الرياضية مثل المتوسط الحسابي والمتوسط المربعي.
6- في علم النفس: يتم استخدام مقياس الوسط الحسابي لتحليل بيانات الاستبيانات والتحليل النفسي.
إذاً، يمكن القول إن مقاييس النزعة لها استخدامات عديدة في حياتنا اليومية في مجالات مختلفة.
ختاماً
بناءً على ما سبق، يمكن القول إن مقاييس النزعة تلعب دوراً هاماً في تلخيص وتحليل البيانات الكمية في مجالات مختلفة. وبالرغم من وجود بعض العيوب في استخدام هذه المقاييس، إلا أنها لا تزال أدوات قيمة في فهم وتحليل البيانات.
لذلك، ينبغي علينا الاستفادة من هذه المقاييس بشكل صحيح ومناسب في حياتنا اليومية لتحسين فهمنا للبيانات واتخاذ القرارات المناسبة بناءً عليها.
مقاييس النزعة المركزية PDF،مقاييس النزعة المركزية والتشتت word،مقاييس النزعة المركزية والتشتت PDF،مقاييس النزعة المركزية والتشتت ppt




