كيف اقرأ تفسير تحليل مربع كاي؟
نحن الآن جاهزون للخطوة الأخيرة ، أي تفسير نتائج تحليل مربع كاي. لهذا سنحتاج إلى فهم جدول توزيع Chi-Square. هذا جدول احتمالية للقيم المختارة لـ X 2 (كيف اقرأ تفسير تحليل مربع كاي)
 (كيف اقرأ تفسير تحليل مربع كاي)
(كيف اقرأ تفسير تحليل مربع كاي)
يحسب الإحصائيون احتمالات معينة لحدوث (قيم P) لقيمة X 2 اعتمادًا على درجات الحرية .درجات الحريةهو ببساطة عدد الفئات التي يمكن أن تختلف بشكل مستقل ناقص واحد ، (ن -1). في هذه الحالة درجات الحرية = 1 لأن لدينا 2النمط الظاهريالطبقات:مقاومةوسريع التأثر. (طريقة حساب مربع كاي)
يمكن مقارنة القيمة المحسوبة لـ X 2 من نتائجنا بالقيم الموجودة في الجدول المتوافقة مع درجات الحرية المحددة لدينا. سيخبرنا هذا باحتمال أن تكون الانحرافات (بين ما توقعنا رؤيته وما رأيناه بالفعل) ناتجة عن الصدفة وحدها ويمكن دعم فرضيتنا أو نموذجنا. (أمثلة على مربع كاي)
في مثالنا ، قيمة X 2 البالغة 1.2335 ودرجات الحرية 1 مرتبطة بـ aقيمة P.أقل من 0.50 ، ولكن أكبر من 0.25. هذا يعني أن قيمة مربع كاي كبيرة أو أكبر (أو الاختلافات بينهمامُتوقعوالأرقام المرصودة بهذا الحجم أو أكبر) يمكن أن تحدث ببساطة عن طريق الصدفة بين 25٪ و 50٪ من الوقت. (كيف اقرأ تفسير تحليل مربع كاي)
وفقًا للاتفاقية ، غالبًا ما يستخدم علماء الأحياء القيمة 5.0٪ (p <0.05) لتحديد ما إذا كانت الانحرافات الملحوظة مهمة. أي انحرافات أكبر من هذا المستوى ستجعلنا نرفض فرضيتنا ونفترض أن شيئًا آخر غير الصدفة كان يلعب.
إذا كانت القيمة المحسوبة لمربع كاي أكبر من القيمة الحرجة لمربع كاي ، فأنت ترفض فرضيتك الصفرية. إذا كانت القيمة المحسوبة لمربع كاي أقل من القيمة الحرجة لمربع كاي ، فإنك “تفشل في رفض” فرضيتك الصفرية.
إيجاد القيمة الاحتمالية لمربع كاي يساوي 1.2335 بدرجة حرية واحدة
اقرأ أولاً العمود 1 لأسفل للعثور على صف درجة الحرية الأولى ثم انتقل إلى اليمين إلى حيث سيحدث 1.2335. هذا يتوافق مع احتمال أقل من 0.5 ولكن أكبر من 0.25 ، كما هو موضح بواسطة الأسهم الزرقاء.
 (كيف اقرأ تفسير تحليل مربع كاي)
(كيف اقرأ تفسير تحليل مربع كاي)
لذلك في مثال تربية الطماطم لدينا ، فشلنا في رفض فرضيتنامقاومةإلى بقعة بكتيرية في هذه المجموعة من الصلبان ناتجة عن واحدة موروثة بشكل سائدالجين(Rx-4). يمكننا أن نفترض أن الانحرافات التي رأيناها بين ما توقعناه وفي الواقعلاحظمن حيث عدد النباتات المقاومة والقابلة للتأثر يمكن أن يكون بسبب مجرد الصدفة.
يمكننا مواصلة العمل مع فرضيتنا الحالية. تذكر أننا لم “نثبت” فرضيتنا في هذه المرحلة. سيتم استخدام المزيد من الاختبارات في التهجينات والمجموعات الأخرى لتقديم دليل إضافي على أن فرضيتنا تشرح بدقة طريقة وراثة Rx-4.
تفسير النتائج الرئيسية لاختبار Chi-Square من أجل الاقتران
أكمل الخطوات التالية لتفسير اختبار خي مربع للارتباط. يتضمن الإخراج الأساسي قيم p ، وعدد الخلايا ، ومساهمة كل خلية في إحصاء مربع كاي. (اختبار مربع كاي PDF)
في هذا الموضوع
- الخطوة 1: تحديد ما إذا كان الارتباط بين المتغيرات ذات دلالة إحصائية
- الخطوة 2: افحص الفروق بين الأعداد المتوقعة والتعداد المرصود لتحديد المستويات المتغيرة التي قد يكون لها أكبر تأثير على الارتباط (كيف اقرأ تفسير تحليل مربع كاي)
الخطوة 1: تحديد ما إذا كان الارتباط بين المتغيرات ذات دلالة إحصائية
لتحديد ما إذا كانت المتغيرات مستقلة أم لا ، قارن القيمة p بمستوى الأهمية. عادةً ما يكون مستوى الأهمية (يُشار إليه بـ α أو alpha) 0.05 جيدًا. يشير مستوى الأهمية البالغ 0.05 إلى وجود خطر بنسبة 5٪ في استنتاج وجود ارتباط بين المتغيرات في حالة عدم وجود ارتباط فعلي.
قيمة P ≤ α: المتغيرات لها ارتباط ذي دلالة إحصائية (رفض H 0 )
إذا كانت القيمة p أقل من أو تساوي مستوى الأهمية ، فإنك ترفض الفرضية الصفرية وتستنتج أن هناك ارتباطًا ذا دلالة إحصائية بين المتغيرات. (كيف اقرأ تفسير تحليل مربع كاي)
P-value> α: لا يمكن استنتاج أن المتغيرات مرتبطة (فشل في رفض H 0 )
إذا كانت القيمة p أكبر من مستوى الأهمية ، فإنك تفشل في رفض فرضية العدم لأنه لا يوجد دليل كافٍ لاستنتاج أن المتغيرات مرتبطة. (حالات استخدام مربع كاي)
اختبار Chi-Square لمربع Chi-Square DF P-Value Pearson 11.788 4 0.019 نسبة الاحتمالية 11.816 4 0.019
النتائج الرئيسية: P-Value لـ Pearson Chi-Square ، P-Value لنسبة الاحتمالية Chi-Square
في هذه النتائج ، فإن إحصاء Pearson chi-square هو 11.788 والقيمة p = 0.019. احتمالية تشي مربع الإحصاء هي 11.816 والقيمة p = 0.019. لذلك ، عند مستوى دلالة 0.05 ، يمكنك استنتاج أن الارتباط بين المتغيرات ذو دلالة إحصائية.
الخطوة 2: افحص الفروق بين الأعداد المتوقعة والتعداد المرصود لتحديد المستويات المتغيرة التي قد يكون لها أكبر تأثير على الارتباط (كيف اقرأ تفسير تحليل مربع كاي)
لتحديد المستويات المتغيرة التي لها أكبر تأثير ، قارن بين الأعداد المرصودة والمتوقعة أو افحص المساهمة في مربع كاي
من خلال النظر في الاختلافات بين عدد الخلايا المرصودة وعدد الخلايا المتوقعة ، يمكنك معرفة المتغيرات التي لها أكبر الاختلافات ، والتي قد تشير إلى التبعية. يمكنك أيضًا مقارنة المساهمات بإحصاء مربع كاي لمعرفة المتغيرات التي لها أكبر القيم التي قد تشير إلى التبعية.
الصفوف: أعمدة المعرف: أعمدة ورقة العمل: الوردية الأولى الوردية الثانية الوردية الثالثة: الكل
1 48 47 48143 56.08 46.97 39.96 1.1637 0.0000 1.6195 2 76 47 32155 60.78 50.91 43.31 3.8088 0.2998 2.9530 3 36 40 34110 43.14 36.13 30.74 1.1809 0.4151 0.3468
الكل 160 134114408 عد محتويات الخلية العدد المتوقع المساهمة في مربع كاي
النتائج الرئيسية: العدد ، العدد المتوقع ، المساهمة في مربع كاي
في هذا الجدول ، عدد الخلايا هو الرقم الأول في كل خلية ، والعدد المتوقع هو الرقم الثاني في كل خلية ، والمساهمة في إحصاء مربع كاي هو الرقم الثالث في كل خلية. في هذه النتائج ، يعد العدد المتوقع والعدد المرصود الأكبر في التحول الأول مع الآلة 2 ، والمساهمة في إحصاء مربع كاي هي الأكبر أيضًا. تحقق من عمليتك أثناء التحول الأول باستخدام الآلة 2 لمعرفة ما إذا كان هناك سبب خاص يمكن أن يفسر هذا الاختلاف. (شرح مربع كاي)
تفسير نتائج مربع كاي في SPSS
سيوضح لك هذا البرنامج التعليمي السريع كيفية تفسير نتيجة حساب مربع كاي الذي أجريته في SPSS.
النتائج
يبدأ البرنامج التعليمي من افتراض أنك قمت بالفعل بحساب إحصاء مربع كاي لمجموعة البيانات الخاصة بك ، وتريد معرفة كيفية تفسير النتيجة التي توصل إليها برنامج SPSS. ( لدينا برنامج تعليمي مختلف يشرح كيفية إجراء اختبار مربع كاي في برنامج SPSS ). (كيف اقرأ تفسير تحليل مربع كاي)
يجب أن تبحث عن نتيجة تبدو مثل هذا في عارض مخرجات SPSS.
 (كيف اقرأ تفسير تحليل مربع كاي)
(كيف اقرأ تفسير تحليل مربع كاي)
تحليل الجداول المذكورة أعلاه هو لمتغيرين فئويين ، الدين والأكل. لكل متغير قيمتان محتملتان: لا ديني ومسيحي لمتغير الدين؛ آكل اللحوم والنباتي لمتغير الأكل.
الفرضية الصفرية لدراستنا الافتراضية هي أن هذه المتغيرات لا ترتبط ببعضها البعض – فهي متغيرات مستقلة. يتيح لنا اختبار مربع كاي اختبار هذه الفرضية.
يحتوي ناتج تحليل الجداول الترافقية على عدد من العناصر. دعونا نلقي نظرة على كل على حدة.
 (كيف اقرأ تفسير تحليل مربع كاي)
(كيف اقرأ تفسير تحليل مربع كاي)
ملخص انجاز الدراسة
كما يوحي اسمه ، فإن ملخص معالجة الحالة هو مجرد ملخص للحالات التي تمت معالجتها عند تشغيل تحليل الجداول الترافقية.. (كيف اقرأ تفسير تحليل مربع كاي)
 (كيف اقرأ تفسير تحليل مربع كاي)
(كيف اقرأ تفسير تحليل مربع كاي)
في مثالنا ، كما ترى أعلاه ، كان لدينا 30 حالة صالحة ، ولا توجد حالات مفقودة. (كيف اقرأ تفسير تحليل مربع كاي)
هذا هو جدول الجداول ، ويقدم الكثير من المعلومات المفيدة لتفسير نتيجة اختبار مربع كاي.
يتضمن جدول الجداول الترافقية لدينا معلومات حول الأعداد المرصودة (ما يسميه SPSS “العدد”) والأعداد المتوقعة.
العد المرصود
العد المرصود هو التردد الملحوظ في خلية معينة من جدول الجداول الترافقية. على سبيل المثال ، يوضح جدولنا أن 5 أكلة لحوم (من إجمالي 16) ليس لديهم دين وأن 3 مسيحيين (من إجمالي 14) نباتيون.
العدد المتوقع
العدد المتوقع هو التردد المتوقع لخلية بافتراض أن الفرضية الصفرية صحيحة. في حالتنا ، فإن الفرضية الصفرية هي أنه لا يوجد ارتباط بين متغير الأكل ومتغير الدين ، مما يعني أن العدد المتوقع هو التردد المتوقع لخلية على افتراض أن الأكل والدين لا يعتمدان على بعضهما البعض. (كيف اقرأ تفسير تحليل مربع كاي)
أهمية التعداد المرصود والمتوقع
إذا كنت تريد أن تفهم نتيجة اختبار مربع كاي ، فعليك الانتباه عن كثب إلى التهم المرصودة والمتوقعة. ببساطة ، كلما تباعدت هذه القيم عن بعضها البعض ، كلما زادت درجة مربع كاي ، زادت احتمالية أن تكون مهمة ، وكلما زاد احتمال رفضنا للفرضية الصفرية واستنتاج أن المتغيرات مرتبطة ببعضها البعض .
إذا نظرت إلى جدول الجداول أعلاه ، سترى أن هناك عددًا أكبر من آكلي اللحوم المسيحيين مما كان متوقعًا إذا كانت الفرضية الصفرية (أن المتغيرات مستقلة) صحيحة ؛ وعدد أقل من النباتيين المسيحيين. وبالمثل ، هناك عدد أكبر من الملحدين النباتيين أكثر مما هو متوقع ، وعدد أقل من الملحدين الذين يتناولون اللحوم. (كيف اقرأ تفسير تحليل مربع كاي)
السؤال هو ما إذا كانت هذه الاختلافات كبيرة بما يكفي للسماح لنا باستنتاج أن متغير الأكل ومتغير الدين مرتبطان ببعضهما البعض. هذا هو المكان الذي تلعب فيه إحصائية مربع تشي.
اختبارات Chi-Square
كما ترى أدناه ، يحسب SPSS عددًا من مقاييس الارتباط المختلفة.
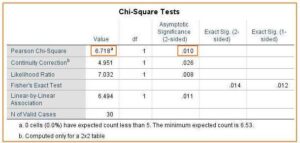
يظهر إحصاء chi square في عمود القيمة مباشرةً على يمين “Pearson Chi-Square”. في هذا المثال ، قيمة إحصاء مربع تشي هي 6.718. (كيف اقرأ تفسير تحليل مربع كاي)
تظهر p -value (.010) في نفس الصف في عمود “Asymptotic Significance (2-sided)”. تكون النتيجة مهمة إذا كانت هذه القيمة مساوية لمستوى ألفا المحدد أو أقل منه (عادةً .05). في هذه الحالة ، تكون قيمة p أصغر من قيمة ألفا القياسية ، لذلك نرفض الفرضية الصفرية التي تؤكد أن المتغيرين مستقلين عن بعضهما البعض. ببساطة ، النتيجة مهمة – تشير البيانات إلى أن المتغيرين الدين والأكل مرتبطان ببعضهما البعض. (كيف اقرأ تفسير تحليل مربع كاي)
يخبرك إحصاء مربع كاي فقط ما إذا كانت المتغيرات مرتبطة أم لا. إذا كنت تريد معرفة كيفية ارتباطهما ، فأنت بحاجة إلى العودة إلى جدول الجداول الترافقية. في مثالنا ، يخبرنا الجدول الترافقي أن الإلحاد مرتبط بشكل غير متناسب بالنباتية وأن تناول اللحوم يرتبط بشكل غير متناسب بالمسيحية.
طالع أيضاً: ما هو معامل ألفا كرونباخ ؟




