معاملات الارتباط
مقدمة
درسنا سابقاً عددًا من مشكلات إعداد البيانات في إنشاء نماذج المعادلات الهيكلية، وفي هذا المقال سنتجاوز إعداد البيانات في وصف الدور المهم الذي يلعبه الارتباط (التباين) في نماذج المعادلات الهيكلية.
نقوم أيضًا بتضمين مناقشة عدد من العوامل التي تؤثر على معاملات الارتباط وكذلك الافتراضات والقيود المفروضة على طرق العلاقات في بناء نماذج المعادلة الهيكلية.
أنواع معاملات الارتباط
وضع فرانسيس جالتون مفهومًا لعملية الارتباط والانحدار لفحص التباين المشترك في سمتين أو أكثر ، وطور كارل بيرسون (1896) المعادلة الإحصائية لمعامل الارتباط والانحدار بناءً على اقتراحه (كروكر وألجينا ، 1986 ؛ فيرغسون وتاكاني) ، 1989 ؛ تانكارد ، 1984). بعد ذلك بوقت قصير ، استخدم تشارلز سبيرمان (1904) إجراء معاملات الارتباط لتطوير تقنية تحليل العوامل.
شكلت معاملات الارتباط والانحدار وتحليل العوامل لعقود عديدة الأساس لتوليد الاختبارات وتحديد البنية الأساسية.
اليوم ، يقوم الباحثون بتوسيع فهمهم للأدوار التي تلعبها معاملات الارتباط ، والانحدار ، وتحليل العوامل في النظرية وإنشاء تعريف لتشمل المتغير الكامن ، وبنية التباين ، ونماذج قياس عامل التأكيد.
إن علاقات ومساهمات جالتون وبيرسون وسبيرمان في مجال الإحصاء ، خاصة معاملات الارتباط والانحدار وتحليل العوامل ، مثيرة للاهتمام .
في الواقع ، لعب أساس معاملات الارتباط بين متغيرين – أي الارتباط أو التباين – دورًا رئيسيًا في الإحصاء.
تسمح معاملات الارتباط الجزئية أيضًا بتحديد العلاقات ذات المتغير الثنائي المحددة بين المتغيرات التي تسمح بتحديد التباين الفريد المشترك بين متغيرين أثناء التحكم في تأثير المتغيرات الأخرى , و يمكن اختبار معاملات الارتباط الجزئية من حيث الأهمية ، على غرار معامل ارتباط بيرسون.
على الرغم من أن معامل ارتباط بيرسون كان له تأثير كبير في مجال الإحصاء ، فقد ظهرت معاملات ارتباط أخرى اعتمادًا على مستوى القياس المتغير.
قدم ستيفنز (1968) خصائص معايير او تصنيفات القياس التي أصبحت تعرف باسم الاسمي والترتيبي والفاصل الزمني والنسبة , و يتم تصنيف أنواع معاملات الارتباط التي تم تطويرها لهذه المستويات المختلفة من القياس في الجدول التالي:
| مستوى القياس ( درجة القياس ) | معاملات الارتباط |
| كلا المتغيرين مفصول | معامل ارتباط بيرسون |
| كلا المتغيرين ترتيبي | معامل سبيرمان , تاو كيندال |
| كلا المتغيرين شكلي | معامل فايالطارىء |
| متغير واحد مفصول , متغير ثنائي التفرع | نقطة ثنائية التسلسل |
| متغير ترتيبي واحد , متغير شكلي واحد | جاما , رتبة ثنائية التسلسل |
| متغير واحد مفصول , متغير اصطناعي واحد | ثنائي التسلسل |
| متغير واحد مفصول , متغير ترتيبي واحد مع استمرارية أساسية | متعدد التسلسل |
| كلا المتغيرين ثنائي التفرع ( شكلي اصطناعي ) | ارتباط رباعي |
| كلاالمتغيرين ترتيبي مع الاستمرارية بشكل اساسي | ارتباط متعدد |
*يشيرالاصطناعي إلى إعادة ترميزالقيم المتغيرة ثنائية.
العديد من برامج الكمبيوتر الشائعة ، على سبيل المثال ، SAS و SPSS ، عادة لا تحسب كل أنواع معاملات الارتباط هذه.
لذلك ، قد تحتاج إلى مراجعة كتاب إحصائي مشهور أو البحث عن برنامج كمبيوتر يحسب نوع معاملات الارتباط الذي تحتاجه – على سبيل المثال ، معامل phi والنقطة ثنائية التسلسل غير متاحين بسهولة.
كما يسمح LISREL بنماذج الخليط ، التي تستخدم متغيرات مع كل من مستويات القياس الترتيبية والفاصلة
على الرغم من أن برامج نماذج المعادلات الهيكلية توضح الآن كيف يمكن تحليل النماذج المتعددة ، إلا أن استخدام المتغيرات ذات المستويات المختلفة للقياس كان يمثل مشكلة في مجال الإحصاء – على سبيل المثال ، الانحدار المتعدد والإحصاءات متعددة المتغيرات.
العوامل المؤثرة في معاملات الارتباط
بالنظر إلى الدور المهم الذي تلعبه معاملات الارتباط في بناء نماذج المعادلة الهيكلية ، نحتاج إلى فهم العوامل التي تؤثر على إنشاء العلاقات بين نقاط البيانات متعددة المتغيرات.
العوامل الرئيسية هي مستوى القياس ، وتقييد النطاق في قيم البيانات (التباين ، والانحراف ، والتفرطح) ، والبيانات المفقودة ، والخطية ، والقيم المتطرفة ، وتصحيح التوهين ، والقضايا المتعلقة بتباين العينة ، وفترات الثقة ، وحجم التأثير ، والأهمية ، والعينة الحجم والقوة.
مستوى القياس ومدى القياس
أربعة أنواع أو مستويات من القياس تحدد عادةً ما إذا كان تفسير المتغير أو مقياسه اسميًا أم ترتيبيًا أم فاصلًا أم نسبة (Stevens، 1968).
في نمذجة ( إنشاء نماذج ) المعادلات الهيكلية ، يمكن استخدام كل نوع من هذه الأنواع من المتغيرات المقاسة. ومع ذلك ، لا يوصى بتضمينهما معًا أو خلطهما في مصفوفة ارتباط (تغاير).
بدلاً من ذلك ، يجب استخدام خيار إخراج بيانات PRELIS لحفظ مصفوفة تعاون مقاربة للإدخال جنبًا إلى جنب مع نموذج مصفوفة التباين – التباين المشترك في برنامج LISREL أو SIMPLIS.
في البداية ، تطلبت نماذج المعادلات الهيكلية المتغيرات المقاسة على مستوى الفاصل الزمني أو النسبة للقياس ، لذلك تم استخدام معامل الارتباط اللحظي للمنتج Pearson في الانحدار والمسار والعامل وانشاء نماذج المعادلة الهيكلية.
يجب أن تحتوي القيم المتغيرة للفاصل الزمني أو النسبة على نطاق كافٍ لقيم الدرجات لإدخال التباين (15 نقطة مقياس أو أكثر).
إذا تم تقييد نطاق الدرجات فسيتم تقليل حجم قيمة الارتباط.
بشكل أساسي ، عندما تصبح مجموعة من الموضوعات أكثر تجانساً ، يقل تباين النقاط ، مما يقلل من قيمة الارتباط بين المتغيرات. كما أن استخدام نفس قيم المقياس للمتغيرات يمكن أن يساعد في تفسير النتائج و / أو المقارنة النسبية بين المتغيرات.
يعتمد معنى علاقة الارتباط على المتغيرات المستخدمة ؛ ومن ثم فإن منظورك النظري والعلمي مهم للغاية , و قد تتذكر من دورة الإحصاء الأساسية الخاصة بك أن الارتباط الزائف ممكن عندما ترتبط مجموعتان من الدرجات بشكل كبير ، لكن علاقتهما ليست ذات مغزى أو موضوعية بطبيعتها.
بعض التحولات المحتملة هي تحويل الجذر التربيعي (sqrt X) ، وتحويل اللوغاريث- (log X) ، والتحويل المتبادل (1 / X) ، وتحويل القوسين (arcsin X).
يبدو أن التحويل المحتمل هو الأكثر فعالية في معالجة البيانات المنحرفة أحادية المتغير.
وبالتالي ، يمكن أن يكون لنوع المقياس المستخدم ونطاق القيم للمتغيرات المقاسة تأثيرات عميقة على تحليلك الإحصائي (على وجه الخصوص ، على المتوسط والتباين والارتباط).
البيانات اللاخطية
يشير معامل ارتباط بيرسون إلى درجة العلاقة الخطية بين متغيرين , و من الممكن أن يشير متغيرين إذا كان لديهم علاقة منحنية إلى عدم وجود ارتباط , وبالتالي ، فإن مدى انحراف المتغيرات عن افتراض وجود علاقة خطية سيؤثر على حجم معامل الارتباط. لذلك من المهم التحقق من خطية الدرجات ؛ الطريقة الشائعة هي رسم نقاط البيانات الإحداثية في مخطط مبعثر.
يمكن إثبات تقييد النطاق في القيم باستخدام مجموعة البيانات الإرشادية الرابعة في الجدول التالي تتراوح قيم Y فقط بين 3 و 7 ، وتتراوح قيم X فقط من 1 إلى 4. ومعامل ارتباط بيرسون هو أيضًا r = 0 لهذه البيانات. تشير مجموعة البيانات الخامسة إلى مدى تأثير أخذ العينات المحدود على معامل بيرسون , و في هذه البيانات النموذجية ، تم أخذ عينات من ثلاثة أزواج فقط من الدرجات ، وكان ارتباط بيرسون هو r = -1.0 ، أو مرتبط بشكل سلبي تمامًا.
مجموعات البيانات الاستكشافية
| البيانات المفقودة | البيانات الكاملة | البيانات غيرالخطية | |||
| y | x | y | x | y | x |
| 8.00 | – | 8.00 | 6.00 | 1.00 | 1.00 |
| 7.00 | 5.00 | 7.00 | 5.00 | 2.00 | 2.00 |
| 8.00 | – | 8.00 | 4.00 | 3.00 | 3.00 |
| 5.00 | 2.00 | 5.00 | 2.00 | 4.00 | 4.00 |
| 4.00 | 3.00 | 4.00 | 3.00 | 5.00 | 5.00 |
| 5.00 | 2.00 | 5.00 | 2.00 | 6.00 | 5.00 |
| 3.00 | 3.00 | 3.00 | 3.00 | 7.00 | 4.00 |
| 5.00 | – | 5.00 | 4.00 | 8.00 | 3.00 |
| 3.00 | 1.00 | 3.00 | 1.00 | 9.00 | 2.00 |
| 2.00 | 2.00 | 2.00 | 2.00 | 10.00 | 1.00 |
| تأثير أخذ العينات | نطاق البيانات | ||
| y | x | y | x |
| 8.00 | 3.00 | 3.00 | 1.00 |
| 9.00 | 2.00 | 3.00 | 2.00 |
| 10.00 | 1.00 | 4.00 | 3.00 |
| 4.00 | 4.00 | ||
| 5.00 | 1.00 | ||
| 5.00 | 2.00 | ||
| 6.00 | 3.00 | ||
| 6.00 | 4.00 | ||
| 7.00 | 1.00 | ||
| 7.00 | 2.00 | ||
بيانات مفقودة
يتغير معامل ارتباط بيرسون من ذو دلالة إحصائية إلى غير ذات دلالة إحصائية.
الأهم من ذلك ، في مصفوفة الارتباط مع العديد من المتغيرات ، يمكن حساب معاملات الارتباط المختلفة على أحجام عينات مختلفة.
إذا استخدمنا الحذف حسب القوائم للحالات ، فإن أي متغير في مجموعة البيانات بقيمة مفقودة قد يتسبب في حذف موضوع ما ، مما قد يتسبب في انخفاض كبير في حجم العينة ، في حين أن الحذف الزوجي للحالات سيؤدي إلى أحجام عينات مختلفة لدينا معاملات الارتباط في مصفوفة الارتباط.
درس الباحثون جوانب مختلفة لكيفية التعامل مع البيانات المفقودة أو معالجتها بما يتجاوز مثالنا التمهيدي باستخدام مجموعة بيانات إرشادية صغيرة. أحد الأساليب الأساسية هو إزالة أي ملاحظات حيث تكون بعض البيانات مفقودة ، وحذفها بطريقة قائمة.
لا يُوصى بحذف القائمة بسبب فقدان المعلومات عن المتغيرات الأخرى ، وتستند التقديرات الإحصائية إلى حجم العينة المصغر, ان الحذف المزدوج يستبعد البيانات فقط عندما تكون مفقودة من أزواج المتغيرات المختارة للتحليل.
ومع ذلك ، يمكن أن يؤدي هذا إلى أحجام عينات مختلفة للارتباطات المختلفة والتقديرات الإحصائية ذات الصلة.
هناك نهج ثالث و هو احتساب البيانات و يستبدل القيم المفقودة بتقدير ، على سبيل المثال : متوسط القيمة على متغير لجميع الأشخاص الذين لم يبلغوا عن أي بيانات لهذا المتغير.
يمكن أن تظهر البيانات المفقودة بطرق مختلفة (Little & Rubin، 1987، 1990) , و هذا يعني عدم وجود بيانات عشوائية تمامًا (MCAR) أن البيانات الموجودة على المتغير X تفتقد إلى القيم غير المرتبطة إحصائيًا بالقيم التي تمت ملاحظتها للمتغيرات الأخرى بالإضافة إلى X.
تصحيح التوهين
تصحيح التوهين هو إجراء إحصائي طوره تشارلز سبيرمان في عام 1904 والذي يستخدم “لتخليص معامل الارتباط من الأثر الضعيف لخطأ القياس” ، وهي ظاهرة تُعرف باسم تخفيف التراجع. في القياس والإحصاء ، يسمى التصحيح أيضًا بالإحباط.
الافتراض الأساسي في نظرية القياس النفسي هو أن البيانات المرصودة تحتوي على خطأ في القياس.
درجة الاختبار (البيانات المرصودة) هي دالة للنتيجة الحقيقية وخطأ القياس.
سيكون لمعامل ارتباط بيرسون قيم مختلفة ، اعتمادًا على ما إذا كان قد تم حسابه باستخدام الدرجات المرصودة أو الدرجات الحقيقية حيث تمت إزالة خطأ القياس.
يمكن تصحيح معامل ارتباط بيرسون من أجل التوهين أو خطأ القياس غير الموثوق به في الدرجات ، مما ينتج عنه ارتباط حقيقي بالدرجات ؛ ومع ذلك ، يمكن أن يصبح معامل الارتباط المصحح أكبر من 1.0! يمكن أن يؤدي انخفاض الموثوقية في المتغيرات المستقلة و / أو التابعة ، إلى جانب الارتباط العالي بين المتغير المستقل والمتغير التابع ، إلى ارتباطات أكبر من 1.0.
على سبيل المثال ، بالنظر إلى ارتباط r = 0.90 بين الدرجات المرصودة في X و Y ، ومعامل موثوقية Cronbach alpha البالغ 0.60 لدرجات X ، ومعامل موثوقية Cronbach alpha البالغ .70 لدرجات Y ، معامل ارتباط Pearson ، المصحح للتوهين (r *) أكبر من 1.0:
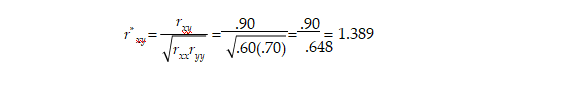
عندما يحدث هذا ، تظهر رسالة خطأ محددة غير موجبة توقف برنامج نماذج المعادلات الهيكلية.
المصفوفات المحددة غير الموجبة
تتسبب معاملات الارتباط الأكبر من 1.0 في مصفوفة الارتباط في أن تكون مصفوفة الارتباط محددة غير موجبة. بمعنى آخر ، الحل غير مقبول ، مما يشير إلى أنه لا يمكن حساب تقديرات المقاييس.
تصحيح التوهين ليس هو الموقف الوحيد الذي يتسبب في حدوث المصفوفات غير الإيجابية (Wothke ، 1993). في بعض الأحيان ، تؤدي نسبة التغاير إلى منتج الفروق المتغيرة إلى ارتباطات أكبر من 1.0.
مصفوفة التباين – التغاير التالية هي غير موجبة محددة لأنها تحتوي على معامل ارتباط أكبر من 1.0 بين متغيرات العلاقات والسمة الكامنة (يُشار إليها بعلامة النجمة):
| مصفوفة التباين والتغاير | ||||
| 1.043 | المهمة | |||
| 1.079 | .994 | العلاقات | ||
| .924 | .905 | .892 | إدارة | |
| 1.12 | .969 | 1.111 | 1.065 | السمة |
| مصفوفة الارتباط | ||||
| 1.000 | المهمة | |||
| 1.000 | .937 | العلاقات | ||
| 1.000 | .906 | .908 | إدارة | |
| 1.000 | .951 | 1.010 | .985 | السمة |
متى تحدث مصفوفات التغاير المحددة غير الموجبة؟
تحدث مصفوفات التغاير المحددة غير الموجبة عندما يكون محدد المصفوفة صفرًا أو يكون معكوس المصفوفة غير ممكن.
يمكن أن يحدث هذا بسبب معاملات الارتباط الأكبر من 1.0 ، التبعية الخطية بين المتغيرات المرصودة ، العلاقة الخطية المتعددة بين المتغيرات الملحوظة ، المتغير الذي هو مزيج خطي من المتغيرات الأخرى ، حجم العينة أقل من عدد المتغيرات ، وجود سلبي أو التباين الصفري (حالة Heywood) ، وقيم التباين – التباين (الارتباط) خارج النطاق المسموح به ، على سبيل المثال ، الارتباط الذي يتجاوز +/ 1.0 ، وقيم البدء السيئة في النموذج المحدد من قبل المستخدم.
تحدث حالة Heywood أيضًا عندما يكون تقدير الجماعة أكبر من 1.0. الحلول الممكنة لحل هذا الخطأ هي تقليل المجتمع أو إصلاح المجتمع إلى أقل من 1.0 ، واستخراج عدد مختلف من العوامل (ربما عن طريق إسقاط المسارات) وتحل نماذج الانحدار والمسار والعامل والمعادلة الهيكلية رياضيًا مجموعة من المعادلات المتزامنة باستخدام تقديرات المربعات الصغرى العادية (OLS) كتقديرات أولية للمعاملات في النموذج.
ومع ذلك ، فإن هذه التقديرات الأولية أو المعاملات تكون في بعض الأحيان مشوهة أو مختلفة للغاية عن الحل النهائي المقبول.
معاملات الارتباط ثنائية المتغير والجزئية
قدم كوهين سنة 1983 في وصف بحث الارتباط مزيدًا من الارتباط بين متغيرين يتحكمان في تأثير متغير ثالث. يشار إلى هذه معاملات الارتباط على أنها ارتباطات جزئية وجزئية ، اعتمادًا على كيفية التحكم في المتغيرات أو استبعادها جزئيًا. يوضح الشكل 3.1 بعض الطرق المختلفة التي يمكن من خلالها تصوير ثلاثة متغيرات. توضح الرسوم البيانية مواقف مختلفة بين المتغيرات حيث (أ) جميع المتغيرات غير مرتبطة (الحالة 1) ، (ب) زوج واحد فقط من المتغيرات مرتبط (الحالات 2 و 3) ، (ج) زوجان من المتغيرات مرتبطان (الحالات 4) و 5) و (د) جميع المتغيرات مترابطة (الحالة 6). من الواضح أنه مع وجود أكثر من ثلاثة متغيرات ، تصبح الاحتمالات هائلة. لذلك من المهم أن يكون لديك منظور نظري لاقتراح سبب ارتباط بعض المتغيرات و / أو التحكم فيها في الدراسة. المنظور النظري ضروري في تحديد نموذج ويشكل الأساس لاختبار نموذج المعادلة الهيكلية.
يقيس معامل الارتباط الجزئي الارتباط بين متغيرين بينما يتحكم في متغير ثالث ، على سبيل المثال ، معاملات الارتباط التالية:
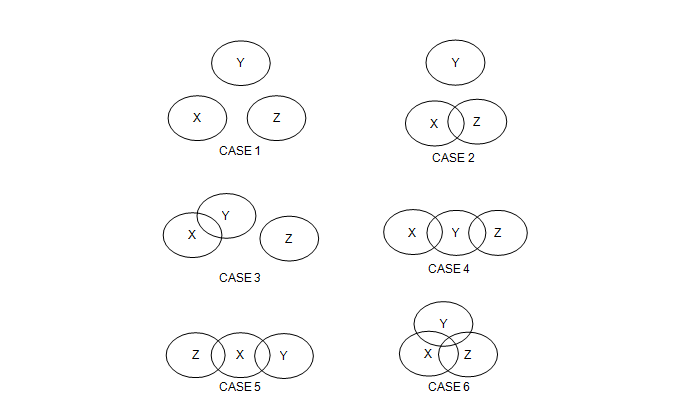
العلاقات الممكنة ثلاثية المتغيرات
الارتباط مقابل التغاير Correlation versus Covariance
نوع مصفوفة البيانات المستخدمة للحسابات في برامج تعديل المعادلات الهيكلية هو مصفوفة التباين والتغاير. تتكون مصفوفة التباين – التغاير من مصطلحات التباين على الشروط القطرية والتغايرية على خارج القطر.
إذا تم استخدام مصفوفة الارتباط كمصفوفة بيانات الإدخال ، فإن معظم برامج الكمبيوتر بشكل افتراضي تقوم بتحويلها إلى مصفوفة التباين والتغاير باستخدام الانحرافات المعيارية للمتغيرات ، ما لم ينص على خلاف ذلك.
الباحث لديه خيار إدخال البيانات الأولية ، أو مصفوفة الارتباط ، أو مصفوفة التباين والتغاير. توفر مصفوفة الارتباط خيار استخدام متغيرات موحدة أو غير قياسية لأغراض التحليل. إذا تم إدخال مصفوفة الارتباط مع صف من المتوسطات المتغيرة (على الرغم من كونها اختيارية) وصف من الانحرافات المعيارية ، يتم استخدام مصفوفة التباين والتغاير مع إخراج غير قياسي.
على سبيل المثال ، مصفوفة التباين – التغاير للمتغيرات الثلاثة التالية ، X و Y و Z ، هي كما يلي:
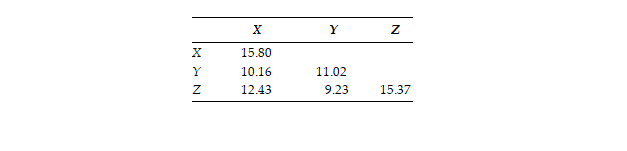
لها 3 (3 + 1) / 2 = 6 قيم مميزة: 3 تباين و 3 شروط تغاير.
يتم حساب معاملات الارتباط باستخدام الفروق والتغاير بين المتغيرات ثنائية المتغير ، باستخدام الصيغة التالية:
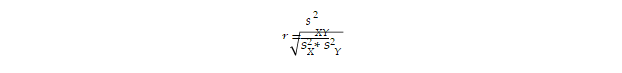
قسمة التغاير بين متغيرين (شروط التغاير هي القيم خارج القطر في المصفوفة) على الجذر التربيعي لمنتج المتغيرين المتباينين (تباينات المتغيرات على قطري المصفوفة) ينتج عنها معاملات الارتباط التالية بين الثلاثة المتغيرات:
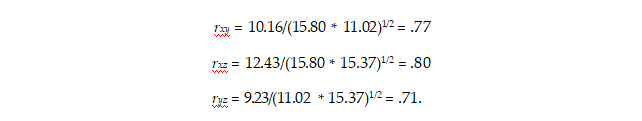
بشكل عام ، يجب استخدام مصفوفة التباين – التغاير في نمذجة المعادلة الهيكلية ، على الرغم من أن بعض نماذج المعادلات الهيكلية تتطلب وسائل متغيرة ، على سبيل المثال ، نماذج الوسائل المنظمة.
المقاييس المتغيرة (موحدة مقابل غير موحدة)
ناقش الباحثون استخدام المتغيرات غير القياسية أو المعيارية (Lomax ، 2007).
يُعتقد أن المعاملات الموحدة هي عينة محددة وغير مستقرة عبر عينات مختلفة بسبب التغيرات في تباين المتغيرات.
تسمح المعاملات غير المعيارية بفحص التغيير عبر عينات مختلفة.
ومع ذلك ، فإن المعاملات الموحدة مفيدة في تحديد الأهمية النسبية لكل متغير للمتغيرات الأخرى لعينة معينة.
الأسباب الأخرى لاستخدام المتغيرات المعيارية هي أن المتغيرات على نفس مقياس القياس ، ويمكن تفسيرها بسهولة أكبر ، ويمكن بسهولة تحويلها مرة أخرى إلى مقياس المقياس الخام.
الافتراضات السببية والقيود والمحددات
كما تمت مناقشته سابقًا ، فإن معامل ارتباط بيرسون محدود بنطاق قيم الدرجات وافتراض الخطية ، من بين أشياء أخرى.
حتى إذا تم استيفاء الافتراضات والقيود الخاصة باستخدام معامل علاقة بيرسون ، فإن علاقة السبب والنتيجة لم تثبت بعد.
الشروط التالية ضرورية لاستنتاج السبب والنتيجة بين المتغيرين X و Y (Tracz ، 1992): (أ) الترتيب الزمني (X يسبق Y في الوقت المناسب) ، (ب) وجود التغاير أو الارتباط بين X و Y ، و (ج) التحكم لأسباب أخرى ، على سبيل المثال ، جزء Z من X و Y.
قد لا تكون هذه الشروط الثلاثة موجودة في تصميم تصميم البحث ، وفي مثل هذه الحالة ، يمكن استنتاج الارتباط فقط وليس السببية. ومع ذلك ، إذا تم استخدام المتغيرات المتلاعبة في الدراسة ، فيمكن للباحث تغيير أو معالجة متغير واحد في الدراسة وفحص التأثيرات اللاحقة على المتغيرات الأخرى ، وبالتالي تحديد علاقات السبب والنتيجة (Resta & Baker، 1972).
توجد اختلافات فلسفية بين افتراض العلاقات السببية مقابل الاستدلال بين المتغيرات ، ويتطلب حل هذه القضايا منظورًا نظريًا سليمًا. قدم بولوك وهارلو ومليك (1994) مناقشة متعمقة لقضايا السببية المتعلقة ببحوث نمذجة المعادلة الهيكلية. نشعر أن نماذج المعادلة الهيكلية ستتطور إلى ما هو أبعد من النموذج المناسب في مجال اختبار النموذج كما تشهد عليه العديد من تطبيقات نماذج المعادلات الهيكلية الجديدة اليوم.
يمكن أن يتضمن اختبار النموذج بدلاً من ملاءمة النموذج اختبار أهمية المعلمات أو تغيير المعلمة أو العوامل الأخرى التي تؤثر على قيم نتائج النموذج والتي يمكن تقييم آثارها.
هذا النهج ، في اعتقادنا ، يصور بشكل أفضل الافتراض السببي. بالإضافة إلى ذلك ، يمكن للنماذج الهيكلية في البحث الطولي أن تصور التغييرات في المتغيرات الكامنة بمرور الوقت (Collins & Horn ، 1992).
الملخص
لا تحسب معظم برامج الكمبيوتر جميع أنواع معاملات الارتباط المستخدمة في الإحصاء ، لذا يجب على القارئ الرجوع إلى كتاب إحصائي معياري للصيغ الحسابية والفهم (Hinkle، Weirsma، & Jurs، 2003؛ Lomax، 2007). تستخدم برامج نمذجة المعادلات الهيكلية مصفوفة التباين والتغاير ، وتتضمن ميزات لإخراج نوع المصفوفات التي تستخدمها.
تم تطوير PRELIS للسماح بمصفوفة ارتباط لأنواع مختلفة من معاملات الارتباط ليتم تكييفها أو تحويلها إلى مصفوفة تغاير مقاربة للمدخلات في برامج نمذجة المعادلات الهيكلية (Jöreskog & Sörbom ، 1993). سيستمر استخدام معاملات الارتباط المختلفة والتحويل اللاحق إلى مصفوفة التباين والتغاير في لعب دور رئيسي في نمذجة المعادلة الهيكلية ، خاصة نماذج المزيج المعينة.
يقوم برنامج نماذج المعادلات الهيكلية أيضًا بتحويل مصفوفات العلاقات ذات الانحرافات المعيارية إلى مصفوفة التباين والتغاير ، ولكن إذا كانت معاملات الارتباط المخففة أكبر من 1.0 ، فستظهر رسالة خطأ محددة غير موجبة بسبب حل غير مقبول. رسائل الخطأ المحددة غير الإيجابية شائعة جدًا بين المبتدئين لأنهم لا يفحصون البيانات ، معتقدين بدلاً من ذلك أن نمذجة المعادلة الهيكلية لن تتأثر.
مصدر قلق رئيسي آخر هو عندما تؤدي التقديرات الأولية لمخطط المربعات الصغرى إلى قيم بداية سيئة للمعاملات في النموذج ؛ ومع ذلك ، فإن تغيير عدد التكرارات الافتراضية في بعض الأحيان يحل هذه المشكلة. يلخص مربع استكشاف الأخطاء وإصلاحها هذه المشكلات
طالع أيضاً: المعادلات الهيكلية (برنامج ليزريل): قضايا ومشاكل إدخال البيانات وتحريرها