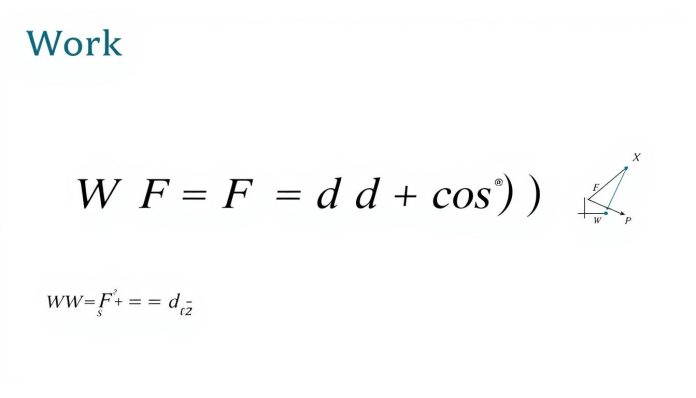الشغل في الفيزياء يُعد مفهومًا أساسيًا. يساعدنا على فهم كيفية انتقال الطاقة بين الأجسام. هذا المقال يُحلل المعادلة الرياضية لحساب الشغل.
العلوم تعرف الشغل بأنه حاصل ضرب القوة في المسافة التي يقطعها الجسم. هذا المفهوم مهم في نظرية النسبية والميكانيكا الكلاسيكية.
النقاط الرئيسية
- الشغل هو كمية الطاقة المنتقلة عند تحريك جسم
- وحدة قياس الشغل هي الجول (J)
- يرتبط الشغل مباشرة بالقوة والمسافة
- يلعب دورًا محوريًا في فهم انتقال الطاقة
- يختلف مقدار الشغل حسب زاوية تأثير القوة
مفهوم الشغل في الفيزياء وأهميته
الشغل هو مفهوم أساسي في الفيزياء. يربط بين القوة والحركة بطريقة دقيقة. يلعب دورًا محوريًا في فهم كيفية انتقال الطاقة بين الأجسام.
يغطي هذا في مجالات مثل ميكانيكا الكم وديناميكا الموائع وديناميكا الحرارة.
التعريف الفيزيائي للشغل
يُعرَّف الشغل بأنه حاصل ضرب القوة المؤثرة في الإزاحة. يقيس كمية الطاقة المنتقلة عندما يتحرك جسم تحت تأثير قوة معينة. يتم حساب الشغل من خلال:
- قياس مقدار القوة المؤثرة
- تحديد المسافة التي يتحركها الجسم
- حساب الزاوية بين اتجاه القوة والحركة
العلاقة بين الشغل والطاقة
الشغل والطاقة مرتبطان بشكل وثيق. عندما يتم بذل شغل، تتحول الطاقة من شكل إلى آخر. في مجالات مثل ديناميكا الموائع، يمكن رؤية هذا التحول بوضوح.
وحدات قياس الشغل
الوحدة الأساسية لقياس الشغل هي الجول (Joule). يمثل الجول الشغل المبذول عند تطبيق قوة مقدارها 1 نيوتن على جسم يتحرك لمسافة 1 متر في اتجاه القوة.
| الوحدة | الرمز | التعريف |
|---|---|---|
| الجول | J | وحدة الشغل والطاقة |
| النيوتن متر | N·m | مرادف للجول |
شغل فيزياء: المعادلة الأساسية والعوامل المؤثرة
فهم حساب الشغل مهم جدًا في الفيزياء. يساعد في دراسة المجالات الكهرومغناطيسية والفيزياء الفلكية. معادلة الشغل تتضمن ثلاثة عوامل رئيسية.
القوة المؤثرة على الجسم
القوة مهمة جدًا في حساب الشغل. إذا كانت القوة أكبر، فإن الشغل المبذول يزداد. في الفيزياء الحديثة، هناك أنواع مختلفة من القوى.
- القوى الثابتة
- القوى المتغيرة
- القوى الخارجية
المسافة التي يقطعها الجسم
المسافة تؤثر بشكل مباشر على الشغل. كلما كانت المسافة أكبر، زاد الشغل المبذول. في الفيزياء الفلكية، هذا يفسر حركة الأجسام.
الزاوية بين القوة والمسافة
الزاوية بين القوة والإزاحة مهمة جدًا. المعادلة W = F × D × cos(θ) توضح تأثيرها.
المعادلة الأساسية: W = F × D × cos(θ)
هذه المعادلة تساعد في فهم العلاقات المعقدة. تسمح بتحليل دقيق للطاقة والحركة.
حالات خاصة في حساب الشغل المبذول
في عالم تطبيقات الفيزياء، يختلف حساب الشغل بحسب العلاقة بين القوة والإزاحة. هناك حالات مميزة تستحق الدراسة والتحليل الدقيق.
- القوة المتعامدة على الإزاحة: يكون الشغل صفرًا
- القوة الموازية للإزاحة: يصل الشغل إلى أقصى قيمته
- القوة المعاكسة للحركة: يظهر الشغل السلبي
في تطبيقات الفيزياء العملية، نجد أمثلة متعددة لهذه الحالات. على سبيل المثال، عندما يدفع شخص جدارًا دون تحريكه، فإن الشغل المبذول يساوي صفر رغم بذل الجهد.
الفهم الدقيق لحالات الشغل يساعد في تحليل الظواهر الفيزيائية بشكل أعمق
تلعب زاوية القوة والإزاحة دورًا حاسمًا في حساب كمية الشغل المنجز. كلما اقتربت الزاوية من الصفر، زادت كمية الشغل المبذول.
الخلاصة
الشغل في الفيزياء يربط بين القوة والحركة والطاقة. من خلال دراسته، نكتشف أهمية فهم كيفية حسابه. هذا يساعد في تطبيقاته في مجالات العلوم والهندسة.
في هذا المقال، نستعرض المعادلة الرياضية للشغل بدقة. نبرز العوامل المؤثرة مثل القوة والمسافة والزاوية. يمكن حساب الشغل بدقة عالية باستخدام المعادلات المناسبة.
نرى كيف يرتبط الشغل بالطاقة. هذا يساعد في فهم الظواهر الفيزيائية المعقدة. من الميكانيكا الكلاسيكية إلى التكنولوجيا الحديثة، الشغل مهم جدًا.
في النهاية، الشغل أداة علمية قوية. يساعد الباحثين والمهندسين في فهم الأنظمة الفيزيائية بشكل أفضل.